Chapter 2: Structure Of Atom – Class 11 Notes for NEET/JEE
We Must Have To Cover These Topics Given Below-
| S. No. | Topic Name |
|---|---|
| 1 | Introduction to Atomic Structure |
| 2 | Discovery of Electron, Proton, and Neutron |
| 3 | Thomson’s Atomic Model |
| 4 | Rutherford’s Nuclear Model & Alpha Scattering Experiment |
| 5 | Bohr’s Atomic Model – Postulates, Radius, Energy, and Limitations |
| 6 | Shells and Subshells |
| 7 | Dual Nature of Matter – de Broglie Equation |
| 8 | Heisenberg’s Uncertainty Principle |
| 9 | Quantum Mechanical Model of Atom |
| 10 | Schrödinger’s Wave Equation (conceptual understanding) |
| 11 | Quantum Numbers (Principal, Azimuthal, Magnetic, Spin) |
| 12 | Shapes of s, p, d Orbitals (basic shape understanding) |
| 13 | Probability Density (ψ²) and Radial Distribution (for JEE) |
| 14 | Aufbau Principle |
| 15 | Pauli’s Exclusion Principle |
| 16 | Hund’s Rule of Maximum Multiplicity |
| 17 | Electronic Configuration of Elements (Z ≤ 30) |
| 18 | Line Spectrum of Hydrogen – Lyman, Balmer, Paschen Series |
| 19 | Rydberg Formula (derivation for JEE, formula for NEET) |
| 20 | Significance of Wave Function (ψ and ψ²) |
| 21 | Nodes (Radial & Angular), Nodal Planes (JEE-focused) |
| 22 | Energy Level Diagrams |
1. Introduction to Atomic Structure
🔹 1. What is an Atom ?
An atom is the smallest unit of matter that cannot be broken further by chemical methods.
It makes up everything — solids, liquids, gases, even our own body!
🔹 2. History of Atom
- The idea of the atom came from ancient Indian and Greek philosophers.
- Democritus (Greek) said that matter is made up of tiny indivisible particles called “atomos”.
- In India, Maharishi Kanad also gave a similar idea — he called it “anu”.
🔹 3. Dalton’s Atomic Theory (1808)
John Dalton was a scientist who gave the first scientific atomic theory.
He said:
- All matter is made of atoms.
- Atoms are indivisible and indestructible.
- All atoms of a given element are identical.
- Atoms combine in fixed whole-number ratios to form compounds.
- Chemical reactions involve rearrangement of atoms.
🟡 Note: Some points of Dalton’s theory are now outdated due to discovery of electrons, protons, and neutrons.
Also You Can Study With Our Notes Chapter 1- . Some Basic Concepts of Chemistry
🔹 4. Subatomic Particles
Later, scientists discovered that the atom is not indivisible — it has smaller parts:
| Particle | Symbol | Charge | Mass (approx.) | Discovered by |
|---|---|---|---|---|
| Electron | e⁻ | –1 | 1/1836 u | J.J. Thomson |
| Proton | p⁺ | +1 | 1 u | Ernest Rutherford |
| Neutron | n⁰ | 0 (neutral) | 1 u | James Chadwick |
🔹 5. Modern Understanding of Atom
- An atom has two main parts:
- Nucleus – center part, contains protons and neutrons
- Electron cloud – electrons revolve around the nucleus in different paths or orbitals
🔹 6. Size of Atom
- Atoms are extremely small.
- Radius of an atom ≈ 10⁻¹⁰ m
- Radius of nucleus ≈ 10⁻¹⁵ m
➡️ This means the nucleus is 10,000 times smaller than the atom!
🔹 7. Mass of Atom
- Almost the entire mass of the atom is in its nucleus because electrons are very light.
- Unit of atomic mass is atomic mass unit (u) or dalton (Da).
1 u = 1/12th of mass of carbon-12 atom.
🔹 8. Atomic Symbols and Numbers
- Atomic Number (Z) = Number of protons = Number of electrons (in neutral atom)
- Mass Number (A) = Number of protons + Number of neutrons
- Representation: AZX
- Example: 612C means Carbon has 6 protons and 6 neutrons
🔹 9. Isotopes, Isobars, Isotones
- Isotopes: Same atomic number, different mass number (e.g. ¹H, ²H, ³H)
- Isobars: Same mass number, different atomic number (e.g. ¹⁴C and ¹⁴N)
- Isotones: Same number of neutrons (e.g. ¹⁴C and ¹⁵N have 8 neutrons)
✅ Quick Summary:
| Concept | Meaning |
|---|---|
| Atom | Smallest unit of matter |
| Dalton’s Theory | First scientific theory of atoms |
| Subatomic Particles | Electron, Proton, Neutron |
| Nucleus | Dense center of atom, contains p⁺ and n⁰ |
| Electron Cloud | Region where e⁻ move around nucleus |
| Atomic Number (Z) | No. of protons (also electrons in neutral atom) |
| Mass Number (A) | Protons + Neutrons |
| Isotopes | Same Z, different A |
| Isobars | Same A, different Z |
| Isotones | Same number of neutrons |
2. Discovery of Electron, Proton, and Neutron
🔹 1. Discovery of Electron
🧠 Discovered by: J.J. Thomson (1897)
🧪 Experiment: Cathode Ray Tube Experiment (Crookes Tube)
✅ Setup:
- A glass tube with low-pressure gas inside.
- Two metal plates (electrodes): Cathode (-) and Anode (+).
- High voltage (~10,000 volts) applied.
🔍 Observations:
- A greenish glow (fluorescent light) observed on the opposite wall.
- Rays travel from cathode to anode, so called “Cathode Rays”.
- These rays:
- Cast shadow of objects placed inside the tube.
- Get deflected by electric and magnetic fields, indicating they are negatively charged.
- Can rotate a paddle wheel → they have mass.
🧾 Conclusions:
- Rays were made of tiny negatively charged particles → called Electrons.
- J.J. Thomson measured the charge-to-mass ratio (e/m) of electron:
- e/m = 1.758×1011 C/kg
🧪 Charge on Electron (by Millikan’s Oil Drop Experiment):
- Value of charge: e = 1.602 × 10−19 Coulombs
- Hence, mass of electron:
- m= e /(e/m) =9.1×10−31 kg
🔹 2. Discovery of Proton
🧠 Discovered by: E. Goldstein (1886)
🧪 Experiment: Canal Ray Experiment
✅ Setup:
- Modified cathode ray tube with holes in cathode.
- Used hydrogen gas inside the tube.
🔍 Observations:
- Rays seen going in opposite direction to cathode rays (from anode to cathode).
- Called “Canal Rays” or “Anode Rays”.
🧾 Conclusions:
- These rays were made of positively charged particles.
- In hydrogen gas, only one proton per atom — hence the particle was named Proton.
📌 Properties of Proton:
| Property | Value |
|---|---|
| Charge | +1 (1.602 × 10⁻¹⁹ C) |
| Mass | 1.672 × 10⁻²⁷ kg (~1 u) |
| Symbol | p⁺ |
🔹 3. Discovery of Neutron
🧠 Discovered by: James Chadwick (1932)
🧪 Experiment: Bombarded beryllium with alpha particles
✅ Setup:
- Alpha particles (⁴He nuclei) fired at beryllium sheet.
- A new type of radiation was emitted — uncharged and penetrating.
- These rays knocked protons out from paraffin wax.
🔍 Observations:
- The radiation had mass but no charge.
- Could not be deflected by electric/magnetic fields → neutral in nature.
🧾 Conclusion:
- A new particle called neutron was discovered.
- It had no charge, but mass ≈ mass of proton.
📌 Properties of Neutron:
| Property | Value |
|---|---|
| Charge | 0 (neutral) |
| Mass | 1.675 × 10⁻²⁷ kg (~1 u) |
| Symbol | n⁰ |
📊 Comparison Table of Subatomic Particles
| Particle | Symbol | Charge | Mass (kg) | Relative Mass | Discovered By |
|---|---|---|---|---|---|
| Electron | e⁻ | –1 (negative) | 9.1 × 10⁻³¹ | 1/1836 | J.J. Thomson |
| Proton | p⁺ | +1 (positive) | 1.672 × 10⁻²⁷ | 1 | E. Goldstein |
| Neutron | n⁰ | 0 (neutral) | 1.675 × 10⁻²⁷ | 1 | James Chadwick |
🧠 Key Points to Remember (NEET + JEE Focus):
| Concept | NEET | JEE |
|---|---|---|
| Electron discovery | Important theory | + Numericals (e/m ratio) |
| Millikan oil drop (charge) | Basic idea | Derivations may come |
| Proton and canal rays | Theory only | Basic questions |
| Neutron discovery | Theory only | Conceptual MCQs |
| Mass and charge of particles | Factual MCQs | Also used in numericals |
3. 🧪 Thomson’s Atomic Model – Explained for NEET & JEE
🔹 Who Proposed the Model ?
- J.J. Thomson in 1904
- After discovering the electron in 1897, he tried to explain how these electrons are arranged inside the atom.
🔸 Background Before Thomson’s Model
- Scientists had discovered electrons (negatively charged particles), but:
- Atom was electrically neutral
- So, there must be positive charge to balance the electrons
- Thomson tried to explain this arrangement of positive and negative charges in an atom.
🍩 Thomson’s Model (Plum Pudding / Watermelon / Raisin Cake Model)
📖 Main Idea:
“Atom is like a spherical ball of positive charge with electrons embedded in it, like seeds in a watermelon or raisins in a pudding.”
📌 Key Postulates (Points):
| No. | Postulate |
|---|---|
| 1. | Atom is a uniform sphere of positive charge. |
| 2. | Electrons are embedded in this positive sphere like raisins. |
| 3. | Overall charge of atom is zero (neutral), because negative & positive charges balance. |
| 4. | Mass of the atom is evenly spread out. |
📊 Visual Representation:
Imagine:
- A big positively charged sphere
- Tiny negatively charged electrons scattered inside it like:
- Raisins in pudding
- Seeds in watermelon
🧠 Diagram of Thomson’s Model (Describe or draw in exam)
Just like Electrons In An Atoms:- + - +
- + - +
- + -
+ - +
(Big positive sphere with small negative electrons)
🔍 Example Analogy:
- Just like:
- Pudding = positive charge
- Raisins = negative electrons
- Atom = positive “dough” with negative “bits” scattered
✅ Successes of Thomson’s Model
- First model to explain:
- Neutrality of atom
- Presence of electrons
- Set the stage for further research
❌ Failures of Thomson’s Model
| Reason | Why It Failed? |
|---|---|
| Couldn’t explain nucleus | Didn’t mention anything about a dense core in atom |
| No explanation for alpha scattering | Couldn’t explain results of Rutherford’s experiment |
| Didn’t explain energy levels | No idea about how electrons move or how energy is absorbed/emitted |
| Stability issue | Couldn’t explain how electrons stay embedded without moving or collapsing |
🔬 Why was it rejected? (Rutherford’s Alpha Scattering Experiment)
- In 1909, Rutherford did the gold foil experiment, which showed:
- Atom has a tiny, dense, positive nucleus
- Most of the atom is empty space
- This totally contradicted Thomson’s model, so it was discarded.
🎯 NEET & JEE Exam Focus
| Concept | NEET Exam | JEE Main/Advanced |
|---|---|---|
| Basic structure and idea | 1–2 theory questions | 1–2 theory + comparison questions |
| Name and analogy (plum pudding) | Often asked in assertion–reason | Sometimes in MCQs |
| Failures of the model | MCQs and comprehension | Conceptual + paragraph type Qs |
| Visual/Diagram based questions | Low chance | High chance in Advanced |
🧠 Quick Summary Table: Thomson’s Atomic Model
| Feature | Description |
|---|---|
| Discovered by | J.J. Thomson (1904) |
| Nickname | Plum Pudding / Watermelon Model |
| Atom Structure | Positive sphere with electrons embedded |
| Charge | Atom is neutral overall |
| Electrons | Fixed inside the positive mass like seeds |
| Main Limitation | No nucleus, no electron movement, instability |
| Rejected By | Rutherford’s Alpha Scattering Experiment (1909) |
📌 Exam Tip:
Always connect Thomson’s model with what came before (Dalton’s) and after (Rutherford’s) to answer assertion-reason, timeline, or model-based questions.
4. Rutherford’s Nuclear Model & Alpha Scattering Experiment
🔹 1. Background
- After J.J. Thomson’s atomic model, there were many unanswered questions, such as:
- Where is the positive charge exactly located?
- Why do electrons not collapse into the nucleus?
- To answer these, Ernest Rutherford conducted a famous experiment in 1909.
🔬 2. Rutherford’s Alpha Particle Scattering Experiment
✅ Setup:
| Part | Description |
|---|---|
| Source | Alpha particles (α) – ⁴₂He²⁺ nuclei (heavy, +2 charge) |
| Target | Thin gold foil (0.00004 cm thick) |
| Detector | Fluorescent screen coated with zinc sulfide (ZnS) |
| Observation Method | Wherever α-particles hit ZnS, tiny flashes (scintillations) appeared. |
🧠 Why Alpha Particles?
- They are heavy, positively charged, and move at high speed.
- Good for testing the distribution of charge and mass inside atoms.
🔍 3. Observations by Rutherford
| Observation | % Particles Affected |
|---|---|
| Most α-particles passed straight through the gold foil. | ~99% |
| Some α-particles were deflected at small angles. | ~0.1% |
| A very few were deflected at large angles or even bounced back. | ~1 in 20,000 |
📌 4. Rutherford’s Conclusions
From the observations, Rutherford gave a new atomic model.
📖 Main Conclusions:
- Atom is mostly empty space
→ Because most α-particles passed through without deflection. - Positive charge is concentrated in a small, dense region
→ Called the nucleus. - Nucleus is very small compared to the size of atom
→ Most of the atom’s volume is empty space. - Electrons revolve around the nucleus in circular paths → like planets around the sun.
🌐 5. Rutherford’s Atomic Model (Planetary Model)
“Atom consists of a positively charged dense nucleus at the center and electrons revolve around it in circular orbits.”
🧠 Key Features of Rutherford’s Model:
| Feature | Description |
|---|---|
| Nucleus | Dense, heavy, positively charged core of the atom |
| Electrons | Revolve around nucleus in circular orbits |
| Atomic Size | Radius of nucleus ≈ 10⁻¹⁵ m ; Radius of atom ≈ 10⁻¹⁰ m (100,000× larger!) |
| Mass Distribution | Almost all mass of atom is in nucleus |
| Charge Distribution | Positive charge concentrated in nucleus |
📊 Diagram of Rutherford’s Model
Like This- e⁻ e⁻
\ /
\ /
[ Nucleus ]
/ \
e⁻ e⁻
(Electrons revolving around a small central nucleus)
❌ 6. Limitations of Rutherford’s Model
| Problem | Explanation |
|---|---|
| Stability issue | According to classical physics, revolving electrons should emit energy and spiral into nucleus — atom would collapse. But atoms are stable! |
| No explanation of energy levels | Didn’t explain why electrons don’t fall or how spectral lines (like hydrogen spectrum) are formed |
| Couldn’t explain hydrogen spectrum | Rutherford’s model failed to explain line spectra observed in emission/absorption |
🧠 7. How Did Bohr Fix It Later?
- Niels Bohr modified Rutherford’s model by introducing:
- Quantized energy levels
- Electrons revolve in fixed orbits without radiating energy
- But that’s a separate topic! 😄
📌 Summary Table: Rutherford’s Nuclear Model
| Feature | Description |
|---|---|
| Scientist | Ernest Rutherford |
| Year | 1909 (experiment), 1911 (model) |
| Experiment | Alpha scattering with gold foil |
| Observations | Most α-particles passed; few deflected; very few rebounded |
| Nucleus | Tiny, dense, positively charged center of atom |
| Electrons | Revolve around nucleus like planets |
| Major Failure | Could not explain stability of atom or atomic spectra |
📚 Quick Memory Hack:
- Empty space = Most α-particles went straight
- Tiny nucleus = Some deflected sharply
- Electrons revolve = Like planets
- Fails classically = Atom should collapse (but doesn’t!)
5. Bohr’s Atomic Model – Postulates, Radius, Energy, and Limitations
🔹 1. Background: Why Bohr’s Model ?
- Rutherford’s model introduced the nucleus and revolving electrons.
- But it failed to explain:
- Why electrons don’t fall into the nucleus?
- Why atoms emit line spectra (like Hydrogen)?
- So, in 1913, Niels Bohr proposed a new model of the atom.
🧠 2. Bohr’s Postulates (Main Assumptions)
🧾 Postulate 1: Stationary Orbits
Electrons revolve around the nucleus in certain fixed circular paths, called orbits or shells (n=1,2,3…).
- These are also called energy levels.
- While moving in these orbits, electrons don’t radiate energy → hence, atoms are stable.
🧾 Postulate 2: Quantization of Angular Momentum
Only those orbits are allowed where the angular momentum (L) of the electron is a whole number multiple of h/2π.
L = mvr = nh/2π(where n = 1, 2, 3…)
- Here:
- m = mass of electron
- v = velocity
- r = radius of orbit
- h = Planck’s constant
- n = orbit number or principal quantum number
🧾 Postulate 3: Emission or Absorption of Energy
Electron jumps from one orbit to another by absorbing or emitting a photon of energy.
ΔE=E2 – E1 =hν
- If electron goes to higher orbit → absorbs energy
- If it falls to lower orbit → emits energy
- ν = frequency of emitted/absorbed light
🌐 3. Important Formulas from Bohr’s Model (For Hydrogen-like Atoms)
Applies to Hydrogen (H), He⁺, Li²⁺… (i.e., single electron species)
✅ Radius of nth orbit (rₙ):
rn= n2h2ϵ0/πme2Z = 0.529 × n2/Z × 10-10
- n = orbit number
- Z = atomic number
- For hydrogen (Z=1):
- r1= 0.529 10-10
✅ Velocity of electron (vₙ):
vn = Ze2/2ϵ0h ⋅ 1/n=2.18×106 ⋅ Z/n m/s
✅ Energy of electron in nth orbit (Eₙ):
E n= me4Z2/−8ϵ20h2n2 = −13.6 ⋅ Z2/n2eV
- Negative sign shows the electron is bound to nucleus.
✅ Frequency of emitted/absorbed radiation:
ΔE = hν =13.6Z2 (1/n211 − 1/n22) eV
✅ Wave Number Formula (Rydberg’s Formula):
νˉ = RZ2 (1/n21 – 1/n22)
- R = 1.097 × 107m−1 (Rydberg constant)
🌈 4. Spectral Series in Hydrogen Atom (NEET + JEE Favourite)
| Series Name | Transition To (n₁) | From (n₂) | Region |
|---|---|---|---|
| Lyman | 1 | 2,3,4… | UV region |
| Balmer | 2 | 3,4,5… | Visible light |
| Paschen | 3 | 4,5,6… | Infrared |
| Brackett | 4 | 5,6,7… | Infrared |
| Pfund | 5 | 6,7,8… | Infrared |
🎯 5. Success of Bohr’s Model
| Point | Description |
|---|---|
| ✅ Explained stability of atom | Electrons in stable orbits don’t radiate energy |
| ✅ Explained hydrogen line spectrum | Balmer, Lyman, etc. series matched with observed values |
| ✅ Introduced quantum concept | First model using quantization in atomic theory |
| ✅ Mathematically accurate (for H) | Calculated energy levels match experiment (for H & H-like ions) |
❌ 6. Limitations of Bohr’s Model
| Problem Area | Limitation |
|---|---|
| 🧪 Multi-electron atoms | Could not explain spectra of atoms with more than 1 electron |
| 🧲 Zeeman/Stark Effect | Couldn’t explain splitting of lines in magnetic/electric fields |
| ↻ Circular orbits | Assumed fixed circular orbits — contradicts quantum mechanics |
| 📦 Heisenberg’s Principle | Violates uncertainty principle (precise path + momentum together) |
| ❌ Doesn’t explain intensities | Why some spectral lines are brighter/weaker — not explained |
🧠 7. Summary Table: Bohr’s Atomic Model
| Feature | Description |
|---|---|
| Scientist | Niels Bohr (1913) |
| Electrons | Revolve in fixed orbits (n=1,2,3…) |
| Energy | Quantized; only certain levels allowed |
| Jumping Electron | Emits or absorbs light when changing orbits |
| Radius of Orbit (rₙ) | ∝ n²/Z |
| Energy of Orbit (Eₙ) | ∝ -Z²/n² |
| Successfully Explained | Hydrogen spectrum, atomic stability |
| Limitations | Doesn’t work for complex atoms, violates modern principles |
✅ Quick Revision Memonic (for Series):
Let’s Buy Pizza Before Party
(Lyman, Balmer, Paschen, Brackett, Pfund)
6. Shells and Subshells
🔹 1. What are Shells ?
- Electrons in an atom revolve in different energy levels or orbits around the nucleus.
- These orbits are called electron shells.
✅ Shells are denoted by :
| Shell Name | Symbol | Principal Quantum Number (n) |
|---|---|---|
| K-shell | n = 1 | 1st energy level |
| L-shell | n = 2 | 2nd energy level |
| M-shell | n = 3 | 3rd energy level |
| N-shell | n = 4 | 4th energy level |
- The value of ‘n’ (principal quantum number) determines the energy of that shell.
📌 Important Properties of Shells :
- Lower n = Lower energy
- Number of electrons in a shell = 2n22n^22n2
| Shell | n | Max Electrons = 2n² |
|---|---|---|
| K | 1 | 2 |
| L | 2 | 8 |
| M | 3 | 18 |
| N | 4 | 32 |
🔸 2. What are Subshells ?
- Each shell is further divided into subshells based on the azimuthal quantum number (ℓ).
- Subshells are regions within a shell where electrons of particular energy and shape are found.
✅ Types of Subshells :
| Subshell | Symbol | Azimuthal Quantum Number (ℓ) | Max Electrons |
|---|---|---|---|
| s | ℓ = 0 | Spherical shape | 2 |
| p | ℓ = 1 | Dumbbell shape | 6 |
| d | ℓ = 2 | Cloverleaf shape | 10 |
| f | ℓ = 3 | Complex shape | 14 |
📘 Subshells within Each Shell:
| Shell (n) | Subshells Present |
|---|---|
| 1 (K) | 1s |
| 2 (L) | 2s, 2p |
| 3 (M) | 3s, 3p, 3d |
| 4 (N) | 4s, 4p, 4d, 4f |
- Subshells increase with n and follow this pattern.
🧪 3. How Many Orbitals in Each Subshell ?
Each subshell contains a set number of orbitals, and each orbital holds 2 electrons.
| Subshell | Orbitals | Electrons (2 per orbital) |
|---|---|---|
| s | 1 | 2 |
| p | 3 | 6 |
| d | 5 | 10 |
| f | 7 | 14 |
🧠 4. Full Shell–Subshell Structure Example
Let’s see how shells and subshells work together using examples:
🔹 Hydrogen (Z = 1):
- Shell: K (n=1)
- Subshell: 1s → 1 electron
🔹 Oxygen (Z = 8):
- Shells: K (n=1), L (n=2)
- Subshells:
- 1s² (2 electrons)
- 2s² (2 electrons)
- 2p⁴ (4 electrons)
- Total = 8 electrons
🔄 5. Order of Filling Subshells (Aufbau Principle)
Electron filling is based on increasing energy:
In This Manner-
2s
2p
3s
3p
4s
3d
4p
5s
4d
5p
6s
...
You can use the “diagonal rule” to remember this:
Like This- 1s
↓
2s → 2p
↓ ↓
3s → 3p → 4s
↓ ↓ ↓
3d → 4p → 5s
↓ ↓ ↓
4d → 5p → 6s
↓ ↓ ↓
4f → 5d → 6p
↓ ↓ ↓
6d → 7p → 8s
🔍 6. Quick Summary Table: Shells vs Subshells
| Feature | Shell | Subshell |
|---|---|---|
| Defined by | Principal quantum number (n) | Azimuthal quantum number (ℓ) |
| Denoted by | K, L, M, N (or n = 1, 2, …) | s, p, d, f |
| Energy Level | Increases with n | Varies within same n |
| Max Electrons | 2n² | s = 2, p = 6, d = 10, f = 14 |
| Shape | Not specified | s = spherical, p = dumbbell, etc. |
🎯 NEET + JEE Focus Tips
| Topic | NEET Level | JEE Level |
|---|---|---|
| Shell & Subshell basics | Must know names, max e⁻ count | Must know quantum number logic |
| Aufbau Rule | Frequently asked in MCQs | May test exceptions (Cr, Cu etc) |
| Orbitals in each subshell | Direct questions | Orbital diagrams asked |
| Quantum numbers | Important | Conceptual + formula based Qs |
📌 Quick Revision Points:
- Shell = main energy level (n = 1,2,3…)
- Subshell = division of shell (s, p, d, f)
- Each subshell has orbitals (s=1, p=3, d=5, f=7)
- Max electrons in orbital = 2
- Max in subshell = orbitals × 2
7. 🌟 Dual Nature of Matter – de Broglie Equation
🔹 1. What is Dual Nature of Matter?
According to modern physics, matter (like electrons) exhibits both:
- Particle-like properties (mass, momentum)
- Wave-like properties (wavelength, interference)
🧠 This concept is known as the dual nature of matter.
🔍 2. Background: Wave Nature of Light
Before understanding matter’s duality, remember:
- Light was once considered only a wave.
- But Einstein proved it also behaves like a particle (photon).
- So, light shows dual nature — both wave and particle behavior.
👉 Then came a big question:
💡 If light (wave) can behave like a particle, can particles (like electrons) behave like waves?
👨🔬 3. Louis de Broglie’s Hypothesis (1924)
- Louis de Broglie, a French physicist, proposed that:
“All material particles, like electrons, have wave properties.”
🔁 Wave–Particle Duality for Matter:
- Moving particles (like electrons, protons) are associated with waves → called de Broglie waves or matter waves.
🧮 4. de Broglie Equation:
The wavelength (λ) of a moving particle is given by:- λ = h/mv
Where:
- λ = de Broglie wavelength (in meters)
- h = Planck’s constant = 6.626×10−34 Js
- m = mass of the particle (in kg)
- v = velocity of the particle (in m/s)
➡️ Also written as: λ = h/p (since momentum p = mv)
🧠 5. Key Concepts from de Broglie Equation
| Concept | Explanation |
|---|---|
| Particle mass ↑ | Wavelength ↓ (heavier particles have shorter wavelengths) |
| Particle speed ↑ | Wavelength ↓ (faster particles have shorter wavelengths) |
| Only moving objects | Matter waves are associated only with moving particles |
| Massless particles (like photons) | Also show wave nature, but follow different rules |
🧪 6. Applications of de Broglie Concept
🔬 Electron Diffraction Experiments:
- When a beam of electrons is passed through a crystal or slit, it shows interference and diffraction, just like waves.
- This proved experimentally that electrons (particles) behave like waves.
💡 Bohr’s Quantization Justified:
- de Broglie explained why only certain orbits are allowed in Bohr’s model.
- He said: Electron’s orbit must contain an integer number of wavelengths.
2πr = nλ ⇒ 2πr = nh/mv
✔️ This matches Bohr’s quantized angular momentum.
📚 7. de Broglie Wavelength – Numerical Example
Q: Find de Broglie wavelength of an electron moving at 2×106 m/s.
(Mass of electron =9.1×10−31 kg)
Answer- λ= 6.626 × 10−34 /9.1×10−31 ×2 × 106 = 3.64×10−10m
🟢 Comparable to X-ray wavelength → shows wave behavior.
🚫 8. Limitations of de Broglie Concept
| Limitation | Explanation |
|---|---|
| Not observable for large bodies | Wavelength becomes extremely small for heavy objects (like a ball) |
| No explanation of wave source | Doesn’t explain why matter shows wave properties |
| Works only for microscopic particles | Only meaningful for electrons, protons, etc. |
🔄 9. Difference: Classical vs Quantum View
| Property | Classical Physics | Quantum Physics (de Broglie) |
|---|---|---|
| Particle Nature | Mass, position, momentum | Also has wave-like properties |
| Wave Nature | Light is wave only | Light and matter both have dual nature |
| Orbitals | Electrons revolve like planets | Electrons exist in wave-like orbitals |
🧠 10. Quick Revision Summary
| Topic | Formula / Point |
|---|---|
| de Broglie Equation | λ=h/mv |
| Planck’s constant | h=6.626×10−34 Js |
| de Broglie for photon | λ = h/p = hc/E |
| Wavelength vs mass/velocity | Inversely proportional |
| Evidence | Electron diffraction, Bohr’s orbits |
🎯 NEET + JEE Tips
| For NEET | For JEE |
|---|---|
| Memorize formula λ=h/mv | Must know derivation logic + numerical Qs |
| Know wave-particle duality concept | Practice logic-based conceptual Qs |
| Application to electron only | Questions on proton, neutron may appear |
| Simple numericals expected | Detailed numericals and application-based Qs |
📝 Extra Concept: de Broglie for Photon
If a particle has no mass (like a photon), then: λ= hc/E (where E=hν)
8. 🌟 Heisenberg’s Uncertainty Principle
🔹 1. What is This Principle?
This principle says:
“We can’t know the exact position and exact speed (momentum) of a tiny particle (like an electron) at the same time.”
⚠️ If we know where the electron is, we cannot know how fast it’s going and vice versa.
🔹 2. Why is This Important ?
In our daily life, we can easily find where a car is and how fast it’s going.
But with very small particles like electrons, it’s not possible.
When we try to see or measure an electron:
- We shine light (photons) on it.
- That light hits the electron and changes its speed or position.
So, just by looking at it, we disturb it.
🔹 3. The Formula:
The uncertainty principle is written as: Δx ⋅ Δp ≥ h/4π
Meaning:
- Δx = how uncertain the position is
- Δp = how uncertain the momentum (mass × velocity) is
- h = Planck’s constant = 6.626 × 10−34 Js
➡️ If you try to make position more accurate, momentum becomes less accurate.
🔹 4. Real-Life Example
Imagine you’re in a dark room and trying to find a ball with a flashlight.
- You shine the light → now you see the ball.
- But when light hits it, the ball moves a little.
So now:
- You saw the ball’s position.
- But because it moved, you can’t tell how fast it was going earlier.
This is just like electrons!
🔹 5. Why Is It Important in Chemistry ?
It explains:
- Why electrons don’t follow fixed circular paths (like Bohr said).
- Instead, they are in cloud-like areas called orbitals.
- We can only say: “There is a high chance of finding the electron here.”
So, quantum mechanics is based on probability, not certainty.
🔹 6. Simple Summary Table
| Term | Meaning |
|---|---|
| Position (Δx\Delta xΔx) | Where the particle is |
| Momentum (Δp\Delta pΔp) | Mass × Speed of the particle |
| Uncertainty | We can’t know both exactly at the same time |
| Formula | Δx ⋅ Δp ≥ h/4π |
| Importance | Explains why electrons don’t have fixed orbits |
🔹 7. Important Points for NEET/JEE
✅ No need to remember derivation — just the formula, but understand the derivation is important.
✅ Understand why electrons don’t stay in fixed orbits.
✅ This supports the modern model of atom (quantum model).
🔹 8. Key Takeaways
- Electrons are very small and fast.
- We cannot know both position and speed at the same time.
- This is not because our tools are weak — it’s because nature works this way.
- Electrons move in orbitals (clouds), not fixed paths.
9. 🌌 Quantum Mechanical Model of Atom
🔹 1. What is Quantum Mechanical Model ?
This is the modern model of an atom.
It is based on:
- Heisenberg’s Uncertainty Principle
- de Broglie’s Wave Nature of Electrons
- Schrödinger’s Wave Equation
⚠️ Unlike Bohr’s model (which said electrons move in fixed circular paths), this model says:
Electrons are found in cloud-like areas called “orbitals,” not fixed orbits.
🔹 2. Why Was This Model Needed ?
Bohr’s model failed to explain:
- Multielectron atoms
- Shapes of molecules
- Why only certain orbitals are allowed
So, scientists developed this model using quantum mechanics (the science of very small particles).
🔹 3. Main Features of the Quantum Mechanical Model
| Feature | Explanation |
|---|---|
| 🔬 Electrons behave like waves | (From de Broglie) |
| 🚫 We can’t know position & momentum exactly | (From Heisenberg) |
| 📊 Electron’s behavior is probabilistic | Not fixed paths, only chances |
| 🌀 Schrödinger’s Equation used | To calculate where electron is most likely to be |
| ☁️ Electrons are in orbitals | Not orbits; they are 3D regions where electron is likely to be found |
🔹 4. Schrödinger’s Wave Equation (Basic Idea)
Erwin Schrödinger gave a mathematical equation that describes the wave behavior of an electron: H^Ψ = EΨ
Don’t worry! You don’t have to solve it in NEET or JEE.
✅ Just understand:
- Ψ\PsiΨ (psi) = wave function
- Ψ2\Psi^2Ψ2 = probability of finding the electron
Wherever Ψ2\Psi^2Ψ2 is large → electron is likely to be found there
This region = orbital
🔹 5. What Are Orbitals ?
Orbitals are 3D regions around the nucleus where the probability of finding the electron is high (about 90-95%).
Important Points:
| Orbital | Description |
|---|---|
| ☁️ Not fixed path | It’s a cloud-like region |
| 🧊 Each orbital has shape | s = spherical, p = dumbbell, etc. |
| 🎯 Maximum 2 electrons | Can stay in one orbital with opposite spins |
🔹 6. Differences: Bohr’s Orbit vs. Quantum Orbital
| Bohr’s Orbit | Quantum Orbital |
|---|---|
| Fixed circular path | 3D cloud-like region |
| Definite position & speed | Only probability known |
| Classical physics based | Quantum mechanics based |
| Works only for H atom | Works for all atoms |
🔹 7. What This Model Explains:
- Why electrons don’t crash into the nucleus
- How atoms absorb/release energy
- Shapes of orbitals (s, p, d, f)
- Energy levels and sublevels
- Rules like Aufbau, Hund, Pauli (for electron filling)
🔹 8. Key Summary Table
| Concept | Meaning |
|---|---|
| Wave Nature | Electrons behave like waves (de Broglie) |
| Uncertainty | Can’t know both position and speed (Heisenberg) |
| Wave Equation | Schrödinger gave equation to find electron’s behavior |
| Orbital | 3D region where electron is likely to be |
| Probability Concept | No fixed path, only chances |
| Orbitals vs Orbits | Orbitals = modern; Orbits = outdated |
🔹 9. Real-Life Analogy (To Understand Easily)
Imagine a bee flying around a flower:
- It doesn’t follow one fixed circle.
- It moves randomly in the area.
- You can’t say exactly where it is at one moment.
But you can say: “It is usually around this flower.”
This is like an electron in an orbital!
🔹 10. NEET + JEE Important Points
| NEET Aspirants | JEE Aspirants |
|---|---|
| Understand orbitals are clouds, not paths | Understand Schrödinger’s equation conceptually |
| Learn shapes of orbitals (s, p, d) | Practice electron configuration and quantum numbers |
| Focus on probabilistic nature of electrons | Be ready for numerical + conceptual questions |
🔹 11. Keywords to Remember
- Wave function (ψ) = Mathematical description of electron
- ψ² = Probability density
- Orbital = Region where electron is likely to be found
- Quantum Mechanics = Math + rules for tiny particles like electrons
🧠 Final Takeaways:
✅ Quantum model is the most accurate atomic model so far.
✅ Based on mathematics, probability, and waves.
✅ It replaces the idea of fixed paths with cloud-like orbitals.
10. 🔮 Schrödinger’s Wave Equation
🔹 1. What Is Schrödinger’s Wave Equation ?
It is a mathematical equation that describes the behavior of an electron as a wave.
This idea came from:
- de Broglie’s theory: Electrons behave like waves
- Heisenberg’s uncertainty: We can’t find exact location of electrons
- So, instead of “where” electron is, we talk about “where it is likely to be”
Schrödinger ne bola:
“Let’s treat the electron like a wave, and use mathematics to find where it might be found.”
🔹 2. The Equation (Don’t Panic 😅)
H^Ψ=EΨ
Here:
- H^ = Hamiltonian operator (energy of the system)
- Ψ (Psi) = wave function
- E = total energy of the electron
📌 You don’t need to solve this equation in NEET/JEE — just understand what it means.
🔹 3. What is Wave Function (Ψ) ?
- It is a mathematical function.
- It does NOT have a direct physical meaning.
- But when you square it: Ψ2=Probability density\Psi^2 = \text{Probability density}Ψ2=Probability density This tells: What is the chance of finding an electron at a particular location?
🔹 4. Physical Meaning of Ψ and Ψ2
| Symbol | Meaning | Physical Interpretation |
|---|---|---|
| Ψ | Wave function | No physical meaning directly |
| Ψ2 | Probability density | High value → high chance of finding electron |
🔹 5. What Did Schrödinger’s Equation Do?
- Gave us orbitals (regions where electron is most likely to be)
- Predicted energy levels of electrons in an atom
- Helped us understand shapes of orbitals (s, p, d, f)
- Replaced Bohr’s fixed orbits with probability clouds
🔹 6. Orbitals: What We Get from Schrödinger
Schrödinger’s equation tells us:
| Output | Meaning |
|---|---|
| Orbitals | 3D regions of high electron probability |
| Energy levels | Energy of each electron in each orbital |
| Shapes of orbitals | s = sphere, p = dumbbell, etc. |
| Orientation | Direction in space (like px, py, pz) |
🔹 7. Visual Understanding
Imagine you’re trying to find a bee in a garden:
- You don’t know its exact location.
- But if you observe for long time, you’ll notice:
👉 “The bee is usually near this flower.”
That’s like Ψ22: It gives you a probable location, not exact.
Same with electrons in atoms. We don’t know exactly where they are — but we know where they’re likely to be.
🔹 8. Summary Table – What You Should Remember
| Concept | Key Point |
|---|---|
| Schrödinger’s Equation | Describes wave nature of electrons |
| Ψ (psi) | Wave function (mathematical) |
| Ψ² | Probability of finding the electron |
| Output of equation | Orbitals, shapes, energies |
| Supports modern atom model | Based on quantum mechanics |
| Fixed paths replaced by orbitals | Electron clouds, not orbits |
🔹 9. NEET & JEE Specific Points
| NEET Focus | JEE Focus |
|---|---|
| No derivation needed | Understand concepts deeply |
| Know meaning of Ψ and Ψ² | Know how orbitals come from this |
| Understand orbitals and their energy | May ask conceptual/numerical questions |
🔹 10. Final Thoughts
✅ Schrödinger’s equation is the heart of modern atomic theory.
✅ It treats the electron as a wave, not just a particle.
✅ We don’t get fixed paths but probability zones = orbitals
✅ This theory matches experimental results = it works!
11. Quantum Numbers (Principal, Azimuthal, Magnetic, Spin)
🔹 What are Quantum Numbers?
Quantum numbers are like a unique address for every electron inside an atom.
They tell us:
- Electron is in which shell
- Electron is in which shape of orbital
- Orbital is pointing in which direction
- Electron is spinning in which way
🔹 Total 4 Quantum Numbers:
| No. | Name of Quantum Number | Symbol | Tells About… |
|---|---|---|---|
| 1. | Principal Quantum Number | n | Shell / energy level |
| 2. | Azimuthal Quantum Number | l | Subshell / orbital shape |
| 3. | Magnetic Quantum Number | ml | Direction of orbital |
| 4. | Spin Quantum Number | ms | Direction of electron spin |
✅ 1. Principal Quantum Number (n)
- Tells the main shell of the electron (like 1st shell, 2nd shell)
- Values: 1, 2, 3, 4, …
- Bigger nnn means:
- Electron is farther from the nucleus
- Electron has more energy
| n | Shell | Name |
|---|---|---|
| 1 | K | Lowest energy |
| 2 | L | Medium energy |
| 3 | M | Higher |
| 4 | N | Higher |
✅ 2. Azimuthal Quantum Number (l)
- Tells the shape of orbital
- Values: 0 to (n – 1)
| l | Subshell | Shape |
|---|---|---|
| 0 | s | Sphere |
| 1 | p | Dumbbell |
| 2 | d | Clover |
| 3 | f | Complex |
👉 Example: If n = 3, then l = 0,1,2 → means s, p, d orbitals are possible.
✅ 3. Magnetic Quantum Number (mₗ)
- Tells the direction in which the orbital is pointing
- Values: from −l to +l
| l (shape) | Possible mₗ values | No. of Orbitals |
|---|---|---|
| 0 (s) | 0 | 1 |
| 1 (p) | -1, 0, +1 | 3 |
| 2 (d) | -2 to +2 | 5 |
| 3 (f) | -3 to +3 | 7 |
✅ 4. Spin Quantum Number (mₛ)
- Tells the spin direction of electron (up or down)
- Only 2 values:
- +1/2 → clockwise spin
- -1/2 → anticlockwise spin
👉 In 1 orbital, only 2 electrons can stay — and both must have opposite spins.
🔹 Example: Oxygen Atom (Z = 8)
Electron configuration:
1s² 2s² 2p (Here 2,2,4 are electrons, oxygen has 8 electrons)
Last electron is in 2p orbital.
| Quantum Number | Value | Meaning |
|---|---|---|
| n | 2 | 2nd shell (L) |
| l | 1 | p orbital (shape) |
| mₗ | -1/0/+1 (any) | Direction |
| mₛ | +½ or −½ | Spin direction |
🔹 Summary Table
| Quantum Number | Symbol | Tells Us |
|---|---|---|
| Principal | n | Energy level / shell |
| Azimuthal | l | Orbital shape (s, p, d, f) |
| Magnetic | mₗ | Orbital’s direction in space |
| Spin | mₛ | Electron spin (+½ or −½) |
💡 Easy Trick:
Quantum Numbers = Electron’s Full Address!
Like:
🏠 Country (n) → City (l) → Street (mₗ) → Flat Number (mₛ)
🎯 NEET & JEE Tips:
| For NEET | For JEE |
|---|---|
| Understand meaning of each quantum number | Learn how to write full set of 4 numbers |
| Know the shapes (s, p, d, f) | Solve basic MCQs with configuration |
| Don’t worry about derivations | Know value rules and restrictions |
12. Shapes of s, p, d Orbitals (basic shape understanding)
Understanding the shapes of orbitals is a key part of Class 11 Chemistry. Orbitals are regions around the nucleus where the probability of finding an electron is highest. Different orbitals have different shapes, and these shapes help us understand how electrons are arranged in atoms.
In this article, we will explore the shapes of s, p, and d orbitals in simple and easy language — especially for NEET and JEE aspirants.
What is an Orbital?
An orbital is a three-dimensional space around the nucleus of an atom where the probability of finding an electron is maximum. Each orbital has a unique shape and orientation in space.
1. s-Orbital – Spherical Shape
- The s-orbital is spherical in shape.
- It is like a round ball or globe.
- The electron cloud is spread equally in all directions.
Key Points:
- Each energy level has only one s-orbital (e.g., 1s, 2s, 3s…).
- The shape remains the same, but the size increases with higher energy levels.
- s-orbitals do not have directionality.
Electrons held: Maximum 2 electrons in each s-orbital.
2. p-Orbitals – Dumbbell Shape
- p-orbitals look like dumbbells or two balloons joined at the center.
- They have two lobes on either side of the nucleus.
Orientations:
There are three p-orbitals:
- Px – along the x-axis
- Py – along the y-axis
- Pz – along the z-axis
These orbitals are identical in shape and energy but differ in direction.
Key Points:
- p-orbitals begin from the second shell (n = 2).
- Each p-orbital can hold 2 electrons → Total 6 electrons in all three p-orbitals.
- Directional in nature (along x, y, and z axes).
3. d-Orbitals – Cloverleaf & Ring Shapes
- d-orbitals have complex shapes.
- Most look like clover leaves (four lobes), and one has a dumbbell with a ring (doughnut shape).
Types of d-Orbitals:
- dxy
- dyz
- dzx
- dx2-y2
- dz2(dumbbell with a ring)
Key Points:
- d-orbitals start from the third energy level (n = 3).
- There are five d-orbitals in each shell from n = 3 onwards.
- Each orbital can hold 2 electrons → Total 10 electrons in d-sublevel.
- The shape helps explain properties of transition elements.

Summary Table: s, p, d Orbitals
| Orbital Type | Shape | No. of Orbitals | Max Electrons | Starts From |
|---|---|---|---|---|
| s | Spherical | 1 | 2 | n = 1 |
| p | Dumbbell | 3(px,py,pz) | 6 | n = 2 |
| d | Cloverleaf/Doughnut | 5 | 10 | n = 3 |
Quick Comparison:
| Feature | s-Orbital | p-Orbital | d-Orbital |
|---|---|---|---|
| Shape | Sphere | Dumbbell | Cloverleaf / Ring |
| Number of Orbitals | 1 | 3 | 5 |
| Directionality | None | Along x, y, z | Complex orientations |
| Maximum Electrons | 2 | 6 | 10 |
| Starts from Shell | n = 1 | n = 2 | n = 3 |
Important Tips for NEET & JEE
Final Words
Understanding the shapes of orbitals helps in knowing how electrons are arranged and how atoms bond with each other. Always remember:
- s is simple and spherical,
- p is dumbbell-shaped and directional,
- d is complex and clover-like.
- NEET Aspirants: Focus on basic shapes and number of orbitals.
- JEE Aspirants: Also learn names like dxy,dz2 and their orientations.
- No need to draw exact diagrams in most questions, but understand the concept well.
13. Probability Density (ψ²) and Radial Distribution (for JEE)
🧪 What is ψ (Psi) in Quantum Mechanics?
- In quantum mechanics, ψ (psi) is the wave function.
- It gives information about the state of an electron in an atom.
- ψ itself has no physical meaning.
But when we square it, we get something useful.
🌌 What is Probability Density (ψ²)?
- ψ² (psi squared) means the square of the wave function.
- It gives the probability density, i.e., how likely it is to find an electron at a specific point in space.
📌 Meaning:
- High ψ² → High chance of finding an electron there.
- Low ψ² → Low chance.
- ψ² is always positive (because it’s a square).
So, Probability Density = ψ² = likelihood of finding electron per unit volume at a point.
🎯 Visual Example (Imagine This):
Imagine the atom is a foggy cloud:
- Where the fog is thicker, the probability density is higher.
- Where it’s lighter, the probability is lower.
That “thickness” at each point is like ψ².
🌀 Radial Probability and Radial Distribution Function
Even though ψ² tells us probability at a point, we are often more interested in the overall probability in a shell (a circular region at a distance from the nucleus).
That’s where Radial Distribution Function helps.
📈 What is Radial Probability Distribution?
- It tells us the total probability of finding an electron at a particular distance (radius r) from the nucleus.
- It is calculated by:
Radial Probability = ψ2⋅4πr2
🔍 Why Multiply by 4πr2 ?
- Because 4πr2 is the surface area of a spherical shell at distance r.
- It converts point-wise probability (ψ²) into total probability in a spherical shell.
🧠 Simple Difference Between ψ² and Radial Distribution:
| Concept | ψ² (Probability Density) | Radial Distribution Function |
|---|---|---|
| Meaning | Probability per unit volume at a point | Total probability in a spherical shell |
| Depends on | ψ (wave function) | ψ² and distance (r) |
| Mathematical Term | ψ² | ψ² × 4πr² |
| Use | For point-wise electron probability | For radial zones like shells |
| Graph Shape | Peaks at center for s-orbital | Peak is not at center (more later) |
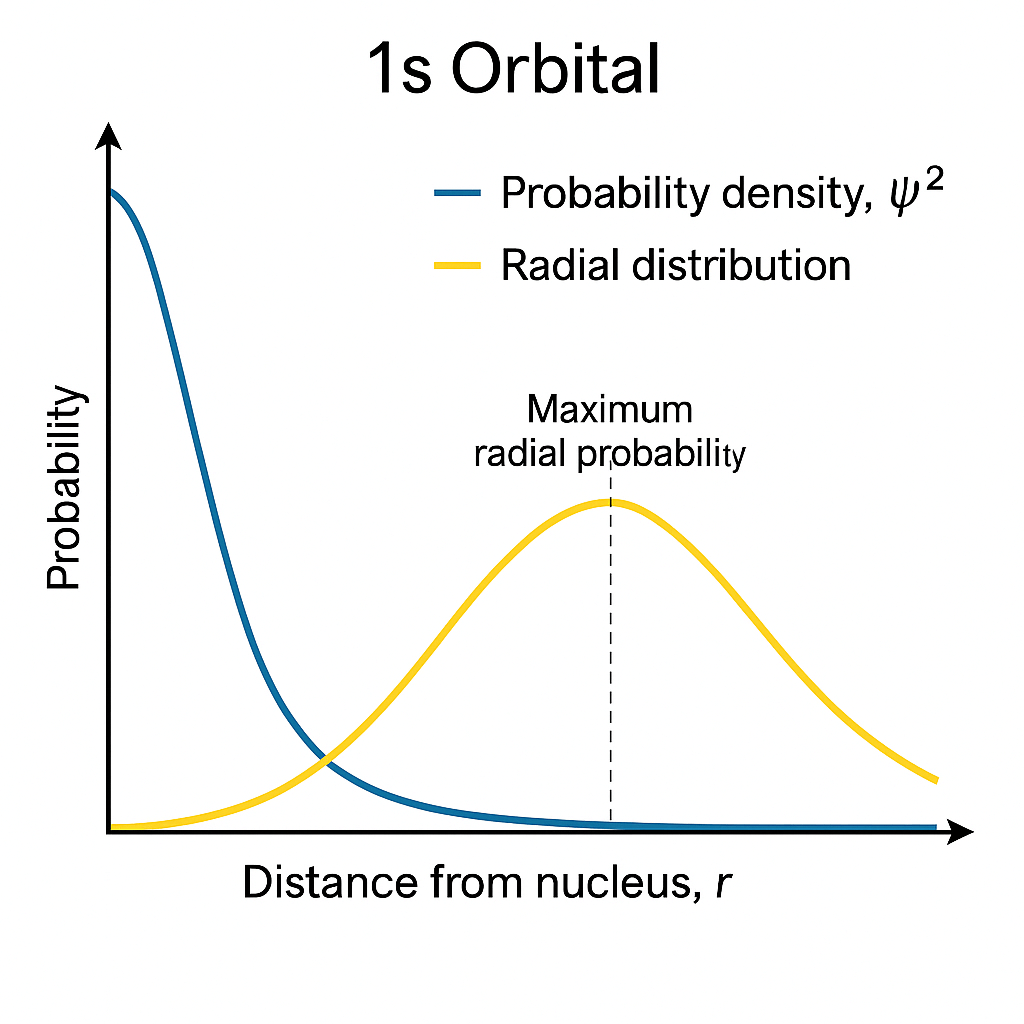
📉 Radial Distribution Graph for 1s Orbital
For 1s orbital (Hydrogen-like atom):
- ψ² is maximum at the nucleus.
- But radial distribution is zero at nucleus, then increases, and then peaks at a certain distance.
That means:
- Although ψ² is highest at the nucleus, the space near the nucleus is very small.
- So the total probability becomes maximum a little away from nucleus.
📊 Graph Summary:
- x-axis: Distance from nucleus (r)
- y-axis: Radial probability
| Region | Behavior |
|---|---|
| At nucleus (r = 0) | ψ² is maximum, but radial distribution is zero |
| At small distance | ψ² still high, and area increases → radial distribution increases |
| At peak distance | Radial distribution is maximum |
| Far away | ψ² becomes small, radial distribution falls |
✅ Important Points for JEE:
- ψ² is the probability density, gives idea at a point.
- Radial distribution considers area at each shell (4πr²).
- Radial probability for 1s orbital is maximum at ~0.53 Å (Bohr radius).
- For higher orbitals (2s, 3s):
- Graph has more than one peak (called nodes).
- The number of nodes = n – l – 1
📌 Definitions (JEE-style):
- Wave Function (ψ): A mathematical function describing the behavior of an electron in an atom.
- Probability Density (ψ²): Square of the wave function; represents the likelihood of finding an electron at a point in space.
- Radial Probability Distribution: Probability of finding an electron at a specific distance (r) from the nucleus in a spherical shell.
- Radial Node: A distance from the nucleus where the radial probability becomes zero.
✍ Example Question for JEE:
Q: In the hydrogen atom, the maximum radial probability for the 1s orbital occurs at:
- (A) r = 0
- (B) r = ∞
- (C) r = a₀
- (D) r = 2a₀
Answer: ✅ (C) r = a₀ (Bohr radius)
📎 Final Summary Table:
| Term | Meaning | Depends On |
|---|---|---|
| ψ (Wave Function) | Mathematical function (no meaning) | n, l, m, r |
| ψ² (Probability Density) | Electron density at a point | ψ |
| Radial Distribution | Total probability in a spherical shell | ψ², 4πr² |
| Radial Node | Point where radial probability is zero | Quantum numbers |
14. 📘 Aufbau Principle
🔷 What is the Aufbau Principle?
The Aufbau Principle explains how electrons are filled in atomic orbitals when building up an atom.
The word “Aufbau” is German for “building up”.
🧠 Definition (Simple):
Electrons enter orbitals starting from the lowest energy level, and go to higher energy orbitals step-by-step.
📌 Why is the Aufbau Principle Important?
Because atoms are most stable when their electrons are in the lowest energy arrangement.
This rule helps us write the correct electronic configuration of any atom.
⚛️ Basic Rules of the Aufbau Principle:
- Electrons fill orbitals in order of increasing energy.
- Lower energy orbitals fill before higher energy ones.
- The order of orbital filling is based on (n + l) rule.
📐 (n + l) Rule – The Key to Order
To find which orbital fills first, calculate the value of n + l:
- n = principal quantum number (main shell: 1, 2, 3,…)
- l = azimuthal quantum number (s = 0, p = 1, d = 2, f = 3)
🧮 How It Works:
- Lower (n + l) → lower energy
- If (n + l) is same for two orbitals, the orbital with lower n fills first
- 3d → n = 3, l = 2 → (n + l) = 5
- 4s → n = 4, l = 0 → (n + l) = 4
➡️ 4s has lower energy than 3d → So, 4s fills before 3d
📊 Order of Orbital Filling (According to Aufbau Principle)
Here’s the correct order in which orbitals are filled:
Like This-
2s
2p
3s
3p
4s
3d
4p
5s
4d
5p
6s
4f
5d
6p
7s
5f
6d
7p
➡️ You can remember this using diagonal rule chart or mnemonic tricks.
📷 Visual Diagram (Diagonal Rule)
Want an image of this? I can generate a diagonal arrow chart for you too!
Some elements do not follow the expected order completely due to extra stability of half-filled or fully-filled orbitals.
Most Common Exceptions:
- Chromium (Cr):
Expected: [Ar] 4s² 3d⁴
Actual: [Ar] 4s¹ 3d⁵ ✔️ (half-filled d orbital is more stable) - Copper (Cu):
Expected: [Ar] 4s² 3d⁹
Actual: [Ar] 4s¹ 3d¹⁰ ✔️ (fully-filled d orbital is more stable)
These happen due to exchange energy and symmetry stability.
🧠 Summary Table:
| Rule | Explanation |
|---|---|
| Aufbau Principle | Fill from lower to higher energy orbitals |
| (n + l) Rule | Lower (n + l) = lower energy |
| Exceptions | Cr, Cu, etc. → due to stable half/full-filled d |
| Electron Configuration Uses | Aufbau + Pauli + Hund’s Rule |
💡 Tips for JEE/NEET:
- Remember the orbital order till at least 6p.
- Practice writing electronic configurations up to atomic number 30.
- Be careful with transition elements — learn their exceptions.
- Always use (n + l) rule if confused.
Q: Which of the following orbitals will fill first?
- (A) 4s
- (B) 3d
- (C) 4p
- (D) 5s
Ans: ✅ (A) 4s (It has lower (n + l) value than 3d)
15. 🧲 Pauli’s Exclusion Principle
🔍 What is Pauli’s Exclusion Principle?
Pauli’s Exclusion Principle is a fundamental rule in quantum mechanics, given by Wolfgang Pauli in 1925.
✅ Statement:
“No two electrons in the same atom can have the same set of four quantum numbers.”
This means that every electron in an atom must be unique in terms of its quantum identity.
To describe the position and properties of an electron, four quantum numbers are used:
| Quantum Number | Symbol | What it Describes | Possible Values |
|---|---|---|---|
| Principal | n | Energy level/shell | 1, 2, 3, … |
| Azimuthal | l | Subshell shape (s, p, d, f) | 0 to (n−1) |
| Magnetic | ml | Orientation of orbital | –l to +l |
| Spin | ms | Spin of electron | +½ or –½ |
According to Pauli, two electrons can never have the same values for all four quantum numbers simultaneously.
🧪 Why is This Important?
The principle explains:
- Why each orbital can hold a maximum of two electrons
- Why those two electrons must have opposite spins (+½ and –½)
- The structure of the periodic table
- The way electrons are arranged in atoms
🔁 Pauli’s Principle and Orbital Filling
Example 1: Helium (Z = 2)
- Electron configuration: 1s²
- Both electrons are in the 1s orbital
- First electron:
n = 1, l = 0, ml = 0, ms = +½ - Second electron:
n = 1, l = 0, ml = 0, ms = –½
✅ All quantum numbers are the same except spin, so this is allowed.
Example 2: Violation
If both electrons in the same orbital had:
- n = 1, l = 0, ml = 0, ms = +½
- n = 1, l = 0, ml = 0, ms = +½
❌ This is not allowed as all quantum numbers are identical.
🎓 Analogy: Cinema Seat Example
Imagine a cinema hall where each seat (orbital) allows only 2 people (electrons).
- Both people must have different ID cards (quantum numbers)
- If one person already occupies a seat with a specific ID (quantum identity), the next person must differ at least in one ID field (spin)
🧬 Link with Electron Configuration
The Pauli principle helps determine:
- How electrons are filled in orbitals
- The maximum number of electrons per orbital (2)
- The structure of electron shells and subshells
🧠 Key Insights for JEE/NEET
| Concept | What It Tells You |
|---|---|
| 1 orbital = max 2 electrons | Because spins must be opposite |
| Every electron is unique | Each has a unique combination of quantum numbers |
| Explains structure of atoms | Especially the periodic table layout |
| Applies to all fermions | Not just electrons but also protons and neutrons |
📊 How Pauli’s Principle Shapes the Periodic Table
The Pauli Exclusion Principle is why the periodic table is structured the way it is. Because:
- Electrons are filled into orbitals one by one
- No two electrons in the same atom can be identical
- This causes a predictable electron configuration pattern
🔄 Pauli vs Hund vs Aufbau – Know the Difference
| Rule | What It Means |
|---|---|
| Pauli’s Exclusion | No 2 electrons can have the same 4 quantum numbers |
| Hund’s Rule | In degenerate orbitals, electrons occupy separately with parallel spins |
| Aufbau Principle | Orbitals are filled in the order of increasing energy |
📝 Sample Questions (JEE & NEET Practice)
🔹 MCQ 1:
Q: How many electrons can occupy the 3p orbital?
A: 6 (3p has 3 orbitals × 2 electrons each = 6)
🔹 MCQ 2:
Q: Which of the following violates Pauli’s Exclusion Principle?
A) 1s²
B) 2s²
C) 2p⁷
D) 3d¹⁰
Answer: C) 2p⁷ (p-subshell can hold a maximum of 6 electrons)
✅ Final Summary – Quick Revision
- Each electron in an atom is identified by 4 quantum numbers.
- No two electrons can have the same set of these 4 quantum numbers.
- Each orbital holds maximum 2 electrons with opposite spins.
- Pauli’s principle is essential for understanding electron configuration, chemical bonding, and the periodic table.
16. 🎯 Hund’s Rule of Maximum Multiplicity
🔍 What is Hund’s Rule?
Hund’s Rule of Maximum Multiplicity explains how electrons are filled into orbitals of the same energy level (called degenerate orbitals) such as p, d, or f subshells.
✅ Hund’s Rule – Statement:
“Electrons occupy all the degenerate orbitals of a subshell singly before pairing begins, and all unpaired electrons in singly occupied orbitals must have the same spin.”
🧠 Key Concepts in Simple Words
- Orbitals within the same subshell (like 2pₓ, 2pᵧ, 2p𝓏) are called degenerate – they have the same energy.
- When electrons are added to such orbitals, each orbital gets one electron first.
- Only after every orbital has one electron, do electrons start pairing.
- Also, these unpaired electrons must all have the same spin (usually ↑).
⚛️ Why Does Hund’s Rule Exist?
- Electrons are negatively charged and repel each other.
- To minimize repulsion, electrons prefer to stay in separate orbitals when possible.
- This leads to more stability and lower energy for the atom.
🔢 Example 1: Nitrogen (Z = 7)
Electron configuration: 1s² 2s² 2p³
The 2p subshell has 3 orbitals (2pₓ, 2pᵧ, 2p𝓏).
We need to place 3 electrons in them.
Correct arrangement (using Hund’s Rule):
2p orbitals:
↑ ↑ ↑
Each orbital gets one electron with parallel spin (same direction).
❌ Incorrect Arrangement (Violates Hund’s Rule):
2p orbitals:
↑↓ ↑ –
This has unnecessary pairing and empty orbitals → unstable.
🔢 Example 2: Oxygen (Z = 8)
Electron configuration: 1s² 2s² 2p⁴
Now we need to place 4 electrons in the 2p orbitals.
Correct arrangement:
2p orbitals:
↑↓ ↑ ↑
- First, 3 electrons go singly into the 3 orbitals.
- The 4th electron pairs with one of them (still follows Hund’s Rule).
🔁 Summary Table
| Hund’s Rule Focus | Explanation |
|---|---|
| Degenerate Orbitals | Orbitals with same energy (e.g., 2pₓ, 2pᵧ, 2p𝓏) |
| Maximum Multiplicity | Maximize the number of unpaired electrons |
| Electron Filling Order | First fill each orbital singly, then pair |
| Spin of Electrons | All unpaired electrons must have the same spin |
🎯 Application in Periodic Table
Hund’s Rule helps explain:
- Magnetic properties (Paramagnetic vs Diamagnetic)
- Stability of half-filled and fully filled subshells
- Shape and structure of orbital diagrams
🔄 Hund’s Rule vs Pauli Exclusion vs Aufbau Principle
| Rule | What It Says |
|---|---|
| Pauli | No 2 electrons in an atom can have same 4 quantum numbers |
| Hund | Electrons fill degenerate orbitals singly first with same spin |
| Aufbau | Electrons fill orbitals in increasing order of energy |
All three rules work together to determine how electrons are arranged in an atom.
📝 Practice Questions (For JEE/NEET)
🔹 MCQ:
Q: Which of the following correctly represents the electron configuration of nitrogen (Z = 7) in 2p orbitals?
(A) ↑↓ ↑ –
(B) ↑ ↑ ↑
(C) ↑↓ – –
(D) ↑↓ ↑↓
Answer: (B)
🔹 Assertion-Reason:
Assertion: Unpaired electrons in degenerate orbitals have the same spin.
Reason: This leads to lower energy due to reduced electron repulsion.
✅ Both Assertion and Reason are true.
✅ Final Summary – Quick Points
- Hund’s Rule applies to orbitals of the same energy level.
- Fill each orbital with one electron first, all with parallel spins.
- Only after that, start pairing the electrons.
- Helps to understand magnetism, reactivity, and stability of elements.
17. Electronic Configuration of Elements (Z ≤ 30)
📘 What is Electronic Configuration?
Electronic Configuration is the arrangement of electrons in an atom’s orbitals.
Each electron in an atom occupies an orbital in a specific order based on:
- Aufbau Principle (electrons occupy orbitals in order of increasing energy),
- Pauli’s Exclusion Principle (no two electrons can have the same 4 quantum numbers),
- Hund’s Rule (electrons occupy degenerate orbitals singly first).
🧠 Orbital Energy Order (Aufbau Sequence)
Electrons fill orbitals in this order:
CopyEdit1s → 2s → 2p → 3s → 3p → 4s → 3d → 4p
💡 Note: Even though 3d comes after 4s in numbering, 4s is filled first because it has lower energy.
⚛️ Maximum Electrons per Subshell:
| Subshell | Maximum Electrons |
|---|---|
| s | 2 |
| p | 6 |
| d | 10 |
| f | 14 |
📍 Format: Electronic Configuration (Z = Atomic Number)
Let’s go from Z = 1 to 30, element by element.
🧪 Z = 1 to 10
| Z | Element | Configuration |
|---|---|---|
| 1 | H | 1s¹ |
| 2 | He | 1s² |
| 3 | Li | 1s² 2s¹ |
| 4 | Be | 1s² 2s² |
| 5 | B | 1s² 2s² 2p¹ |
| 6 | C | 1s² 2s² 2p² |
| 7 | N | 1s² 2s² 2p³ |
| 8 | O | 1s² 2s² 2p⁴ |
| 9 | F | 1s² 2s² 2p⁵ |
| 10 | Ne | 1s² 2s² 2p⁶ |
🔹 Neon (Z=10) is a noble gas → completed 2nd shell.
🧪 Z = 11 to 18
| Z | Element | Configuration |
|---|---|---|
| 11 | Na | 1s² 2s² 2p⁶ 3s¹ |
| 12 | Mg | 1s² 2s² 2p⁶ 3s² |
| 13 | Al | 1s² 2s² 2p⁶ 3s² 3p¹ |
| 14 | Si | 1s² 2s² 2p⁶ 3s² 3p² |
| 15 | P | 1s² 2s² 2p⁶ 3s² 3p³ |
| 16 | S | 1s² 2s² 2p⁶ 3s² 3p⁴ |
| 17 | Cl | 1s² 2s² 2p⁶ 3s² 3p⁵ |
| 18 | Ar | 1s² 2s² 2p⁶ 3s² 3p⁶ |
🔹 Argon (Z=18) is a noble gas → completed 3rd shell.
🧪 Z = 19 to 30 (Includes Transition Metals)
| Z | Element | Configuration |
|---|---|---|
| 19 | K | [Ar] 4s¹ |
| 20 | Ca | [Ar] 4s² |
| 21 | Sc | [Ar] 3d¹ 4s² |
| 22 | Ti | [Ar] 3d² 4s² |
| 23 | V | [Ar] 3d³ 4s² |
| 24 | Cr | [Ar] 3d⁵ 4s¹ ✅ (exception) |
| 25 | Mn | [Ar] 3d⁵ 4s² |
| 26 | Fe | [Ar] 3d⁶ 4s² |
| 27 | Co | [Ar] 3d⁷ 4s² |
| 28 | Ni | [Ar] 3d⁸ 4s² |
| 29 | Cu | [Ar] 3d¹⁰ 4s¹ ✅ (exception) |
| 30 | Zn | [Ar] 3d¹⁰ 4s² |
⚠️ Exceptions You MUST Remember:
Some elements do not follow the expected order due to extra stability of half-filled (d⁵) and fully-filled (d¹⁰) d-orbitals:
| Element | Expected Configuration | Actual Configuration | Why? |
|---|---|---|---|
| Cr (Z=24) | [Ar] 3d⁴ 4s² | [Ar] 3d⁵ 4s¹ ✅ | Half-filled d-subshell |
| Cu (Z=29) | [Ar] 3d⁹ 4s² | [Ar] 3d¹⁰ 4s¹ ✅ | Fully-filled d-subshell |
🔍 Important NEET & JEE Notes
- Know exceptions (Cr and Cu) – highly tested in exams.
- Be comfortable using noble gas shorthand notation.
- Understand how configuration affects valency, magnetism, and chemical reactivity.
🧠 Quick Memory Tip (Order of Orbitals):
Use the diagonal rule or memorize this sequence:
python-replCopyEdit1s
2s 2p
3s 3p
4s 3d 4p
5s 4d 5p
...
➡ Fill diagonally from top to bottom.
📝 Practice Question Examples
MCQ 1:
Q: What is the electron configuration of Calcium (Z = 20)?
A) [Ne] 3s² 3p⁶ 3d²
B) [Ar] 4s²
C) [Ne] 3s² 3p⁶
D) [Ar] 3d²
✅ Answer: B
MCQ 2:
Q: Chromium shows unusual electron configuration due to:
A) Stability of half-filled p-orbitals
B) Stability of half-filled d-orbitals
C) Paired electrons are unstable
D) Hund’s rule violation
✅ Answer: B
✅ Final Summary
- Z ≤ 30 covers elements from Hydrogen to Zinc.
- Use Aufbau, Pauli, and Hund’s rules for correct configurations.
- Know and understand exceptions like Cr and Cu.
- Use noble gas notation to simplify long configurations.
- These configurations affect an element’s properties, bonding, and position in the periodic table.
18.🌈 Line Spectrum of Hydrogen: Lyman, Balmer, Paschen Series
🔍 What is the Line Spectrum ?
When a hydrogen atom’s electron jumps from a higher energy level (n₂) to a lower energy level (n₁), it emits energy in the form of light.
This light is not continuous — it appears as distinct lines of different colors or wavelengths. This is called the line spectrum.
These lines form specific series, each corresponding to a particular region of the electromagnetic spectrum.
⚛️ Why Does Hydrogen Show Line Spectrum?
- Hydrogen has only one electron, which can absorb or emit energy.
- When excited, the electron jumps to a higher energy level (n₂).
- It then falls back to a lower level (n₁), releasing energy as a photon (light).
- The wavelength (or frequency) of this light corresponds to a specific color or type of electromagnetic radiation.
🧪 Formula for Line Spectrum
The Rydberg formula is used to calculate the wavelength (λ) of emitted light:
1/ λ = RH ( 1/ n21−1/n22)
Where:
- λ= wavelength of emitted light
- RH = Rydberg constant = 1.097 × 10⁷ m⁻¹
- n1 = lower energy level (fixed for each series)
- n2 = higher energy level (n2>n1)
🔢 Important Spectral Series of Hydrogen
Let’s understand the 3 major series — Lyman, Balmer, and Paschen — with their energy level transitions and regions.
1️⃣ Lyman Series
| Feature | Details |
|---|---|
| n1=1n_1 = 1n1=1 | Electron falls to first shell |
| n2=2,3,4…n_2 = 2, 3, 4…n2=2,3,4… | From higher shells |
| Region | Ultraviolet (UV) |
| Example Transition | 2 → 1, 3 → 1, 4 → 1… |
📌 Lyman series lies in the ultraviolet region, so it is invisible to human eyes.
2️⃣ Balmer Series
| Feature | Details |
|---|---|
| n1=2n_1 = 2n1=2 | Electron falls to second shell |
| n2=3,4,5…n_2 = 3, 4, 5…n2=3,4,5… | From higher shells |
| Region | Visible light |
| Example Transition | 3 → 2, 4 → 2, 5 → 2… |
📌 Balmer series is the only series visible to the human eye (shows as colored lines).
3️⃣ Paschen Series
| Feature | Details |
|---|---|
| n1=3n_1 = 3n1=3 | Electron falls to third shell |
| n2=4,5,6…n_2 = 4, 5, 6…n2=4,5,6… | From higher shells |
| Region | Infrared (IR) |
| Example Transition | 4 → 3, 5 → 3, 6 → 3… |
📌 Paschen series lies in the infrared region, so it is not visible to the human eye.
📊 Summary Table of Hydrogen Spectral Series
| Series | n1n_1n1 | n2n_2n2 values | Region of Spectrum | Visible to Eye? |
|---|---|---|---|---|
| Lyman | 1 | 2, 3, 4… | Ultraviolet (UV) | ❌ No |
| Balmer | 2 | 3, 4, 5… | Visible | ✅ Yes |
| Paschen | 3 | 4, 5, 6… | Infrared (IR) | ❌ No |
| Brackett | 4 | 5, 6, 7… | Infrared (IR) | ❌ No |
| Pfund | 5 | 6, 7, 8… | Infrared (IR) | ❌ No |
👉 You only need to focus on Lyman, Balmer, and Paschen for Class 11 & NEET/JEE.
🧠 Key Concept: Energy Level Diagram
Here’s a simple representation of energy levels and series:
n=6 ─┬─────────────┐
│ │
n=5 ─┼─────────────┼───> Paschen (to n=3)
│ │
n=4 ─┼─────────────┼───> Balmer (to n=2)
│ │
n=3 ─┼─────────────┼───> Lyman (to n=1)
│ │
n=2 ─┼─────────────┘
│
n=1 ─┘
- Each jump to a lower energy level emits a photon of specific energy.
- The greater the energy difference, the shorter the wavelength of the emitted photon.
🔥 Energy vs Wavelength
- Lyman series → Highest energy → Shortest wavelength (UV)
- Balmer series → Medium energy → Medium wavelength (Visible)
- Paschen series → Low energy → Longer wavelength (IR)
🧪 Real-World Applications
- Spectroscopy: Identifying hydrogen in stars and distant galaxies.
- Astrophysics: Studying the composition and temperature of celestial bodies.
- Atomic models: Basis of Bohr’s model and quantum theory.
📝 NEET / JEE Practice Questions
MCQ 1:
Q: Which transition in hydrogen gives a line in the visible region?
A) n=3 → n=1
B) n=2 → n=1
C) n=4 → n=2
D) n=5 → n=3
✅ Answer: C (Balmer series)
MCQ 2:
Q: The spectral series of hydrogen that lies in the ultraviolet region is:
A) Balmer
B) Paschen
C) Lyman
D) Brackett
✅ Answer: C
✅ Final Summary
- Hydrogen emits line spectra due to electron transitions between energy levels.
- Lyman Series: UV region (n₂ → 1)
- Balmer Series: Visible region (n₂ → 2)
- Paschen Series: IR region (n₂ → 3)
- Use the Rydberg formula to calculate wavelength.
- Important in quantum theory, astrophysics, and spectroscopy.
19. 🌊 Significance of Wave Function (ψ and ψ²)
🔍 What is a Wave Function (ψ) ?
In quantum mechanics, the wave function (ψ) is a mathematical expression that describes the quantum state of a particle, like an electron in an atom.
It was introduced by Erwin Schrödinger in his famous wave equation: H^ψ=Eψ\hat{H} \psi = E \psiH^ψ=Eψ
Where:
- ψ = wave function
- H^ = Hamiltonian operator (total energy)
- E = total energy of the system
⚠️ Note: ψ has no direct physical meaning, but it contains all the information about the state of the electron.
🧠 Physical Meaning Lies in ψ² (psi squared)
Although ψ itself does not have a physical meaning, its square, that is, ψ² (read as “psi squared”), is very important.
🔵 What Does ψ² Represent?
👉 ψ² gives the probability density.
In simple words:
ψ2 = Probability of finding the electron in a small region of space
That means:
- Where ψ² is large, the chance of finding the electron is high.
- Where ψ² is small or zero, the chance is low or none.
✅ So, ψ² tells us where the electron is most likely to be found around the nucleus.
🎯 Example: The Hydrogen Atom
In the hydrogen atom:
- The electron is not orbiting like a planet.
- Instead, it exists as a cloud of probability.
- This cloud is shaped by the values of ψ².
This concept is the foundation of the electron cloud model.
📚 Key Terms Explained
🔸 Probability Density (ψ²)
The likelihood of finding an electron at a point in space.
🔸 Orbital
A region in space where ψ² is significant (not zero). It’s where the electron is most likely to be found.
🔄 Summary Table
| Symbol | Meaning | Physical Meaning? | Unit |
|---|---|---|---|
| ψ | Wave function | ❌ No direct meaning | Depends on system |
| ψ² | Probability density | ✅ Yes (has meaning) | Probability/volume |
📊 Graphical Idea
Imagine a 3D cloud around the nucleus:
- At the center (near nucleus), ψ² is highest → electron is more likely here.
- As you move away, ψ² decreases.
- At some distances, ψ² becomes zero → electron is never found there (called nodes).
⚛️ Node and ψ²
- A node is a region where ψ² = 0
- That means the electron has zero probability of being present there.
Types of nodes:
- Radial nodes (spherical)
- Angular nodes (planar or conical)
🧪 Significance in Chemistry
Why is ψ² important for chemists and physicists?
- It helps visualize atomic orbitals.
- It predicts chemical bonding and molecular shapes.
- It explains electron density and reactivity.
🧠 Real-Life Analogy
Imagine you’re playing hide-and-seek with an invisible friend in a room:
- ψ² gives you a map showing where your friend is most likely to be hiding.
- Darker regions = high chance (more probability)
- White areas = zero chance (nodes)
📝 NEET & JEE Question Examples
MCQ 1:
Q: The physical significance of ψ² is:
A) Velocity of electron
B) Momentum of electron
C) Probability of finding the electron
D) Energy of electron
✅ Answer: C
MCQ 2:
Q: At a node, the value of ψ² is:
A) Maximum
B) Minimum
C) Zero
D) Infinite
✅ Answer: C
✅ Final Summary
| Term | Meaning |
|---|---|
| ψ | Mathematical function — no direct meaning |
| ψ² | Probability density — tells us where electron is likely to be found |
| Node | Point where ψ² = 0 (electron is never found) |
- ψ² is the real hero in quantum mechanics — used to determine electron clouds, orbitals, and atomic structure.
20. 🧠 Nodes, Radial & Angular Nodes, and Nodal Planes
🔍 What is a Node?
A node is a point or region in an atomic orbital where the probability of finding an electron is zero.
In other words: ψ2= 0 at nodes
There are two main types of nodes:
- Radial Nodes (also called spherical nodes)
- Angular Nodes (also called nodal planes)
⚛️ Total Number of Nodes
For any orbital defined by quantum numbers: Total Nodes = n−1
Where:
- n = principal quantum number
- l = azimuthal (angular momentum) quantum number
Then:
Number of Radial Nodes = n−l−1
Number of Angular Nodes=l
📘 Example Table: Total, Radial, and Angular Nodes
| Orbital | n | l | Total Nodes = n−1 | Angular Nodes = l | Radial Nodes = n−l−1 |
|---|---|---|---|---|---|
| 1s | 1 | 0 | 0 | 0 | 0 |
| 2s | 2 | 0 | 1 | 0 | 1 |
| 2p | 2 | 1 | 1 | 1 | 0 |
| 3s | 3 | 0 | 2 | 0 | 2 |
| 3p | 3 | 1 | 2 | 1 | 1 |
| 3d | 3 | 2 | 2 | 2 | 0 |
| 4d | 4 | 2 | 3 | 2 | 1 |
🔴 1. Radial Nodes (Spherical Nodes)
- Definition: A radial node is a spherical surface around the nucleus where the probability of finding the electron is zero.
- Radial nodes depend on both n and l:
Radial nodes=n−l−1
- Present in s, p, d, and f orbitals when nnn is large enough.
📌 Example:
- In the 2s orbital (n=2, l=0):
Radial nodes=2−0−1=1
🟢 2. Angular Nodes (Nodal Planes)
- Definition: An angular node is a plane or cone-shaped region passing through the nucleus where the electron probability is zero.
- Angular nodes depend only on the azimuthal quantum number:
Angular nodes=l\text{Angular nodes} = lAngular nodes=l
| Orbital Type | l | Angular Nodes (nodal planes) |
|---|---|---|
| s | 0 | 0 |
| p | 1 | 1 |
| d | 2 | 2 |
| f | 3 | 3 |
🧠 What are Nodal Planes ?
- Nodal planes are a type of angular node.
- They are flat 2D planes where ψ2= 0 , i.e., electrons cannot exist.
🔸 Example:
- In a p-orbital:
- The shape is dumbbell.
- There is 1 nodal plane (angular node).
- For 2pₓ, the nodal plane is the yz-plane.
- In a dₓy orbital:
- There are 2 nodal planes: xz and yz.
🎨 Visual Summary
| Orbital | Shape | Angular Nodes (Nodal Planes) |
|---|---|---|
| 2s | Spherical | 0 |
| 2pₓ | Dumbbell (along x) | yz-plane |
| 3dₓy | Cloverleaf | xz-plane and yz-plane |
📘 JEE-Level Concept Points
- Nodes are regions of zero electron density.
- Radial nodes are spherical shells, found in all orbitals depending on n−l−1.
- Angular nodes are planar or conical, determined by lll.
- Orbitals with same n but different l have different numbers of angular nodes.
- Total nodes = radial + angular nodes
📝 Practice Questions (JEE Style)
MCQ 1:
Q: The number of radial and angular nodes in a 3p orbital are:
A) 1, 1
B) 2, 0
C) 1, 2
D) 0, 3
✅ Answer: A
(3p: n = 3, l = 1 → Radial = 3 − 1 − 1 = 1; Angular = 1)
MCQ 2:
Q: The total number of nodes for a 4d orbital is:
A) 3
B) 2
C) 4
D) 5
✅ Answer: A
(4d: n = 4, l = 2 → Total nodes = 4 − 1 = 3)
✅ Final Summary
| Type | Formula | Shape | Depends On |
|---|---|---|---|
| Total Nodes | n−1 | – | Principal quantum number |
| Radial Nodes | n−l −1 | Spherical | n and l |
| Angular Nodes | l | Planar/conical | Only l |
- Nodal Planes = Angular Nodes = Plane-shaped regions of zero probability.
21. ⚡ Energy Level Diagrams
🔍 What is an Energy Level Diagram?
An Energy Level Diagram is a graphical representation of the energy of atomic orbitals arranged in increasing order of energy.
It shows:
- How electrons fill orbitals
- The relative energy of orbitals
- Helps understand electronic configuration
🧠 Why Do We Need Energy Level Diagrams?
Because electrons occupy the lowest energy orbitals first (as per the Aufbau Principle), we need to know the energy order of the orbitals.
But — orbitals do not always fill in numerical order (1, 2, 3…).
For example:
- The 4s orbital is filled before the 3d orbital
- This happens due to overlapping of energy levels
So, an energy level diagram helps avoid mistakes.
📘 Key Rules That Govern the Diagram
1. Aufbau Principle
Electrons fill orbitals starting from the lowest energy to the highest.
Filling Order (Based on Energy):
1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s …
2. Pauli’s Exclusion Principle
Each orbital can hold a maximum of 2 electrons, with opposite spins.
3. Hund’s Rule of Maximum Multiplicity
Electrons fill degenerate orbitals (same energy, like p, d, f) singly first before pairing.
🎯 Aufbau Order (Diagonal Rule Method)
You can remember the energy filling sequence using the Diagonal Rule.
🔻 How It Works:
Like This- 1s
↓
2s → 2p
↓ ↓
3s → 3p → 4s
↓ ↓ ↓
3d → 4p → 5s → 4d
↓ ↓ ↓ ↓
5p → 6s → 4f → 5d → 6p
↓ ↓ ↓ ↓ ↓
7s → 5f → 6d → 7p
Just follow the arrows diagonally downward to get the filling order.
🔋 Energy Level Diagram (Up to Z = 30)
Orbitals (With Their Electron Capacities)
| Orbital | Max Electrons |
|---|---|
| 1s | 2 |
| 2s | 2 |
| 2p | 6 |
| 3s | 2 |
| 3p | 6 |
| 4s | 2 |
| 3d | 10 |
| 4p | 6 |
Up to atomic number 30 (Z = 30), orbitals fill as:
→ 1s → 2s → 2p → 3s → 3p → 4s → 3d → 4p
📊 Energy Level Diagram (Visual Representation)
Like This- 1s
↑↓ 2s
↑↓ ↑↓ ↑↓ 2p
↑↓ 3s
↑↓ ↑↓ ↑↓ 3p
↑↓ 4s
↑↓ ↑↓ ↑↓ ↑↓ ↑↓ 3d
↑↓ ↑↓ ↑↓ 4p
- Each arrow ↑ or ↓ represents one electron with spin.
- Orbitals of same type (p, d, f) have multiple sub-levels (3 for p, 5 for d).
🧪 Energy Comparison Between Orbitals
| Orbital | Relative Energy |
|---|---|
| 1s | Lowest |
| 2s | ↑ |
| 2p | ↑ |
| 3s | ↑ |
| 3p | ↑ |
| 4s | ↑ |
| 3d | ↑ |
| 4p | ↑ (Highest among these) |
Note: Even though 3d has n = 3, it is higher in energy than 4s. That’s why 4s fills before 3d.
🧠 Key Concepts for JEE/NEET
- Orbitals are filled based on increasing energy, not order of n.
- Use (n + l) rule to compare orbital energies.
🔸 (n + l) Rule
- Lower n+ln + ln+l = lower energy
- If same n+ln + ln+l, then lower n = lower energy
| Orbital | n | l | n + l |
|---|---|---|---|
| 4s | 4 | 0 | 4 |
| 3d | 3 | 2 | 5 |
→ 4s is filled before 3d
📝 JEE/NEET Question Examples
MCQ 1:
Q: Which orbital is filled just after 3p?
A) 4p
B) 3d
C) 4s
D) 5s
✅ Answer: C (4s)
MCQ 2:
Q: Which of the following orbitals has the highest energy among these?
A) 3s
B) 3p
C) 4s
D) 3d
✅ Answer: D (3d)
MCQ 3:
Q: Which of the following will be filled first?
A) 4s
B) 3d
✅ Answer: A (4s)
(Use the (n + l) rule: 4s = 4, 3d = 5)
🔚 Final Summary
| Concept | Rule/Explanation |
|---|---|
| Aufbau Principle | Fill orbitals from lower to higher energy |
| Pauli’s Principle | Max 2 electrons per orbital with opposite spins |
| Hund’s Rule | Degenerate orbitals fill singly first, then pair |
| (n + l) Rule | Lower (n + l) = lower energy |
| Filling Order | 1s → 2s → 2p → 3s → 3p → 4s → 3d → 4p (for Z ≤ 30) |
For Important Questions & Answer, Message On Instagram→ Learn Sufficient Notes

